The Beauty of Floyd's cycle finding Algorithm of a Linked List
Why am I writing a blog on this topic?
Floyd's cycle finding Algorithm or Tortoise and Hare Algorithm or Fast and Slow pointer method is a pattern used while Solving linked lists and graph questions. When I first encountered the problem cycle detection in a linked list, I didn't get the whole idea of this algorithm for that entire day. After brainstorming and reading a few articles on this topic, I got the point. "Why am I writing this blog ?", this topic was mindblowing and I felt like this is the application of basic algebra in real life. The intuition and logic behind this algorithm is obvious, even an infant can understand the intuition behind it. But I felt the complexity while integrating it with linked lists.
What is this algorithm all about?
The intuition is not complicated, Imagine you are running on a circular race track of length 'L'. You are running at a speed of 'X' per second. Now, Imagine you have your best friend running with you and he is running at a speed of '2*x'. Assume that you guys are starting from the same point in the circular race track.
As the race track is circular, It is clear that you guys will meet at some point. This is Floyd's cycle finding algorithm.
How does this works?
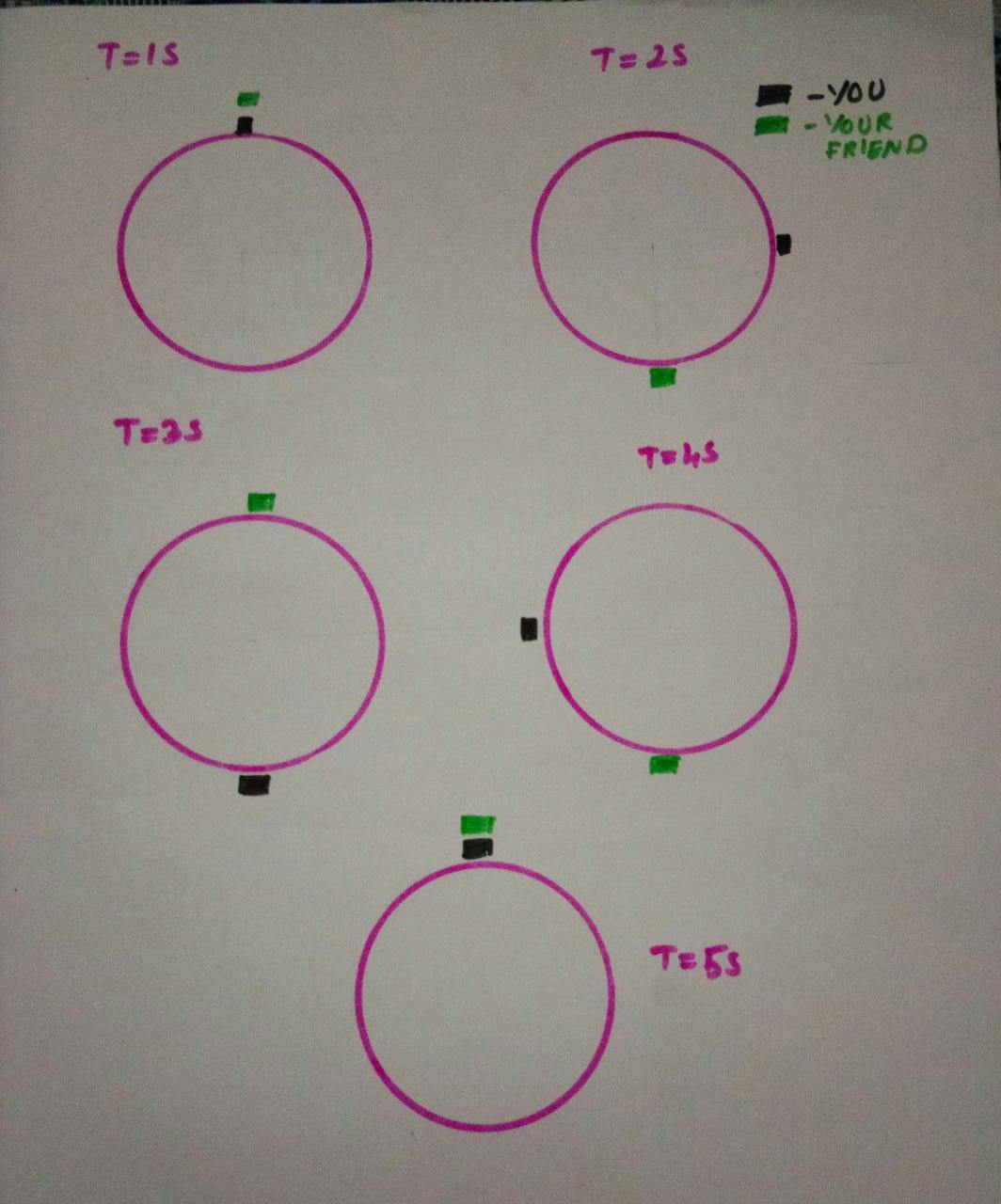
Let the length of the race track be 4 meters and your speed is 1 meter/second. So your friend's speed would be 2 meters/second.
Time = 0th second
You = 0 meter
Your Friend = 0 meter
Time = 1st second
You = 1 meter
Your Friend = 2 meter
Time = 2nd second
You = 2 meter
Your Friend = 4 meter
As your friend reached the end of the track he would've to run through the track once again.So Your Friend = 0
Time = 3rd second
You = 3 meter
Your Friend = 2 meter
Time = 4th second
You = 4 meter
Your Friend = 4 meter
Tadaa!!! Now you guys are at the same point.
How does this work with Linked Lists?
Imagine if you have linked list node with the next pointer pointing towards one of its previous nodes then it forms a cycle or a paradox. When you try to traverse through a linked list you will repeatedly keep traversing the same cycle again and again. Inorder to avoid this problem this method is used.
If you are interested in applying this to code, the checkout these leetcode questions
Linked List Cycle
Linked List Cycle II
Why I found this Algorithm beautiful?
The fact that the simple equation y=2x can explain the above problem was kinda exciting to me!!!